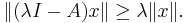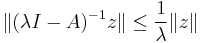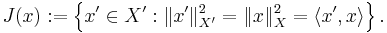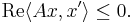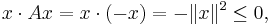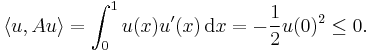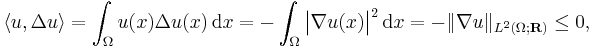Dissipative operator

In mathematics, a dissipative operator is a linear operator A defined on a linear subspace D(A) of Banach space X, taking values in X such that for all λ > 0 and all x ∈ D(A)

$\|(\lambda I-A)x\|\geq\lambda\|x\|.$

A dissipative operator is called maximally dissipative if it is dissipative and for all λ > 0 the operator λI − A is surjective.

The main importance of dissipative operators is their appearance in the Lumer–Phillips theorem which characterizes maximally dissipative operators as the generators of contraction semigroups.

1 Properties
2 Equivalent characterization
3 Examples
4 Notes
5 References

Properties

A dissipative operator has the following properties^[1]

λI − A is injective for all λ > 0 and

$\|(\lambda I-A)^{-1}z\|\leq\frac{1}{\lambda}\|z\|$

for all z in the range of λI − A.

λI − A is surjective for some λ > 0 if and only if it is surjective for all λ > 0. In that case one has (0, ∞) ⊂ ρ(A) (the resolvent set of A).
A is a closed operator if and only if the range of λI − A is closed for some (equivalently: for all) λ > 0.

Equivalent characterization

Define the duality set of x ∈ X, a subset of the dual space X' of X, by

$J(x):=\left\{x'\in X':\|x'\|_{X'}^2=\|x\|_{X}^2=\langle x',x\rangle \right\}.$

By the Hahn–Banach theorem this set is nonempty. If X is reflexive, then J(x) consists of a single element. In the Hilbert space case (using the canonical duality between a Hilbert space and its dual) it consists of the single element x.^[2] Using this notation, A is dissipative if and only if^[3] for all x ∈ D(A) there exists a x' ∈ J(x) such that

${\rm Re}\langle Ax,x'\rangle\leq0.$

Examples

For a simple finite-dimensional example, consider n-dimensional Euclidean space Rⁿ with its usual dot product. If A denotes the negative of the identity operator, defined on all of Rⁿ, then

$x \cdot A x = x \cdot (-x) = - \| x \|^{2} \leq 0,$

so A is a dissipative operator.

Consider H = L²([0, 1]; R) with its usual inner product, and let Au = u′ with domain D(A) equal to those functions u in the Sobolev space H¹([0, 1]; R) with u(1) = 0. D(A) is dense in L²([0, 1]; R). Moreover, for every u in D(A), using integration by parts,

$\langle u, A u \rangle = \int_{0}^{1} u(x) u'(x) \, \mathrm{d} x = - \frac1{2} u(0)^{2} \leq 0.$

Hence, A is a dissipative operator.

Consider H = H₀²(Ω; R) for an open and connected domain Ω ⊆ Rⁿ and let A = Δ, the Laplace operator, defined on the dense subspace of compactly supported smooth functions on Ω. Then, using integration by parts,

$\langle u, \Delta u \rangle = \int_\Omega u(x) \Delta u(x) \, \mathrm{d} x = - \int_\Omega \big| \nabla u(x) \big|^{2} \, \mathrm{d} x = - \| \nabla u \|_{L^{2} (\Omega; \mathbf{R})} \leq 0,$

so the Laplacian is a dissipative operator.

Notes

^ Engel and Nagel Proposition II.3.14
^ Engel and Nagel Exercise II.3.25i
^ Engel and Nagel Proposition II.3.23

References

Engel, Klaus-Jochen; Nagel, Rainer (2000). One-parameter semigroups for linear evolution equations. Springer.
Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. pp. 356. ISBN 0-387-00444-0. (Definition 11.25)